.png "Cyrus–Beck Line Clipping Algorithm using Python") |
| icons taken from pngpath.com |
A generalized line cutting algorithm is the Cyrus–Beck algorithm. It was created to outperform the Cohen–Sutherland algorithm, which relies on repetitive clipping. Unlike Cohen–Sutherland, which can only be used on a rectangular clipping area, Cyrus–Beck is a universal approach that can be used with a convex polygon clipping window.
Read Cohen Sutherland line clipping algorithm in Python, Liang Barsky line clipping algorithm in Python, and Weiler Atherton Polygon Clipping Algorithm in Python. Sutherland Hodgeman polygon clipping algorithm.
Python code for Cyrus–Beck Line Clipping Algorithm
import PIL.ImageDraw as ID, PIL.Image as Image
import numpy as np
# Code Start from here
# Requirement
# pip install pillow
# im will show the overlapped between lines
# im1 will show the clipped line
im = Image.new("RGB", (640, 480))
im1 = Image.new("RGB", (640, 480))
draw = ID.Draw(im)
draw2 = ID.Draw(im1)
draw.polygon((200, 50, 250, 100, 200, 150, 100, 150, 50, 100, 100, 50), outline=255)
draw2.polygon((200, 50, 250, 100, 200, 150, 100, 150, 50, 100, 100, 50), outline=255)
vertices = [[200, 50], [250, 100], [200, 150], [100, 150], [50, 100], [100, 50]]
n = 6
def dot(x1, y1, x2, y2):
return x1 * x2 + y1 * y2
def CyrusBeckLineClipping(x1, y1, x2, y2):
normal = [[0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0]]
for i in range(0, n):
normal[i][1] = vertices[(i + 1) % n][0] - vertices[i][0]
normal[i][0] = vertices[i][1] - vertices[(i + 1) % n][1]
dx = x2 - x1
dy = y2 - y1
dp1e = [[0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0]]
for i in range(0, n):
dp1e[i][0] = vertices[i][0] - x1
dp1e[i][1] = vertices[i][1] - y1
numerator = [0, 0, 0, 0, 0, 0]
denominator = [0, 0, 0, 0, 0, 0]
for i in range(0, n):
numerator[i] = dot(normal[i][0], normal[i][1], dp1e[i][0], dp1e[i][1])
denominator[i] = dot(normal[i][0], normal[i][1], dx, dy)
t = [0, 0, 0, 0, 0, 0]
tE = np.array([0])
tL = np.array([1])
for i in range(0, n):
t[i] = float(numerator[i]) / float(denominator[i])
if denominator[i] > 0:
tE = np.append(tE, t[i])
else:
tL = np.append(tL, t[i])
temp0 = np.amax(tE)
temp1 = np.amin(tL)
if temp0 > temp1:
return
New_X1 = float(x1) + float(dx) * float(temp0)
New_Y1 = float(y1) + float(dy) * float(temp0)
New_X2 = float(x1) + float(dx) * float(temp1)
New_Y2 = float(y1) + float(dy) * float(temp1)
draw2.line((New_X1, New_Y1, New_X2, New_Y2), fill=(0, 255, 0))
def clippingProcess(x1, y1, x2, y2):
draw.line((x1, y1, x2, y2), fill=(0, 255, 0)) #color of the line
CyrusBeckLineClipping(x1, y1, x2, y2)
if __name__ == '__main__':
x1 = int(input("x1: "))
y1 = int(input("y1: "))
x2 = int(input("x2: "))
y2 = int(input("y2: "))
clippingProcess(x1, y1, x2, y2)
im.show()
im.save('Before clipping using Cyrus-Beck.png')
im1.show()
im1.save('After clipping using Cyrus-Beck.png')
Input
x1: 30
y1: 40
x2: 300
y2: 400
y1: 40
x2: 300
y2: 400
Output
 |
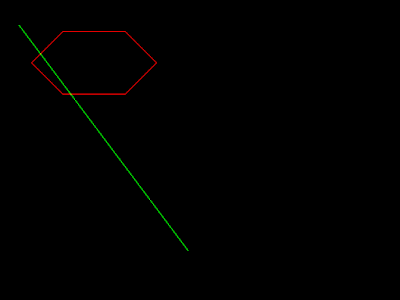| Before Clipping |
 |
| After Clipping |
Read more articles with python solutions in Computer graphics