Midpoint Ellipse Drawing algorithm in computer graphics in python

 Midpoint Ellipse Drawing algorithm

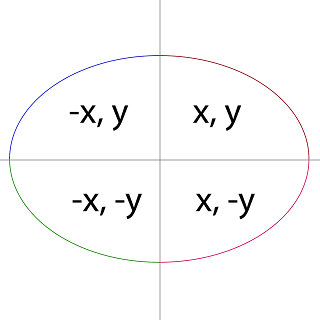
The midpoint ellipse algorithm is one of the algorithms to draw the ellipse algorithm only using addition, subtraction, and multiplication operator. This algorithm is the modified version of Bresenham's circle algorithm. The midpoint ellipse algorithm uses the 4-connected path algorithm instead of the 8-connected path algorithm. The operational and minimum path algorithm makes the midpoint ellipse drawing algorithm faster than others circle algorithms in computer graphics.

There are two parts to draw a Midpoint ellipse algorithm. This will be filled up one by one. This region filling is done in the implementation code of python (region_1, region_2).

1. Region 1

2. Region 2

Code for Midpoint Ellipse Drawing algorithm in python

from PIL import Image as img

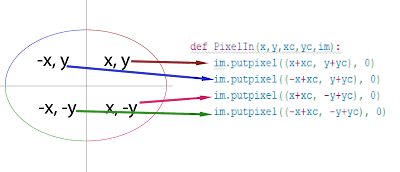
def PixelIn(x,y,xc,yc,im):
   im.putpixel((x+xc, y+yc), 0)
   im.putpixel((-x+xc, y+yc), 0)
   im.putpixel((x+xc, -y+yc), 0)
   im.putpixel((-x+xc, -y+yc), 0)

def midpointellipse(r_x, r_y, xc, yc):
   im = img.new(mode='1', size=(1000, 1000), color=1)
   x = 0
   y = r_y
   region_1 = ((r_y * r_y) - (r_x * r_x * r_y) + (0.25 * r_x * r_x))
   dx = 2 * r_y * r_y * x
   dy = 2 * r_x * r_x * y
   while (dx < dy):
      PixelIn(x,y,xc,yc,im)
      if (region_1 < 0):
         x += 1
         dx = dx + (2 * r_y * r_y)
         region_1 = region_1 + dx + (r_y * r_y)
      else:
         x += 1
         y -= 1
         dx = dx + (2 * r_y * r_y)
         dy = dy - (2 * r_x * r_x)
         region_1 = region_1 + dx - dy + (r_y * r_y)

   region_2 = (((r_y * r_y) * ((x + 0.5) * (x + 0.5))) + ((r_x * r_x) * ((y - 1) * (y - 1))) - (r_x * r_x * r_y * r_y))

   while (y >= 0):
      PixelIn(x,y,xc,yc,im)
      if (region_2 > 0):
         y -= 1
         dy = dy - (2 * r_x * r_x)
         region_2 = region_2 + (r_x * r_x) - dy
      else:
         y -= 1
         x += 1
         dx = dx + (2 * r_y * r_y)
         dy = dy - (2 * r_x * r_x)
         region_2 = region_2 + dx - dy + (r_x * r_x)
   im.save('Midpoint Elipse Output.png')
   im.show()


if __name__=='__main__':
   midpointellipse(280, 200, 500, 500)

Output:

Side to side comparison between the regions in graph and implementation