General knowledge of divergence
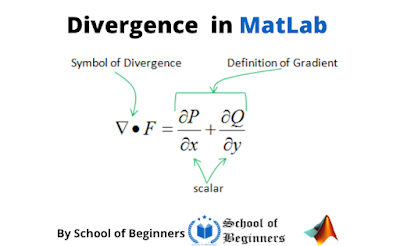
Divergence is a vector operator that operates on a vector field to produce a scalar field that contains the quantity of the vector field's source at each point. In other words, the divergence is the volume density of a vector field's outward flux from an infinitesimal volume around a particular point.
 |
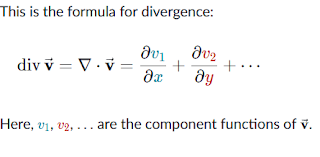| Formula of divergence |
Find divergence of this x + 2y2 – 3z3 vector field in MatLab
solution's code
% Declaring the symbolic variables
syms x y z
% Express the function
f = [x 2*y^2 -3*z^3];
% Evaluating divergence of f
g = divergence(f,[x,y,z]);
% diplaying divergence of f
disp('Divergence of function f is = ')
disp(g)Output
Divergence of function f is =
- 9*z^2 + 4*y + 1
Find divergence of a vector field in MatLab with a proper figure that represents the divergence vector field
solution's code
% Initializing variables
syms x y z
% inputs
% [x 2*y^2 3*z^3]
% [x^2 y^2 z^2]
f = input ('Enter a vector field: '); % [xi,yj,zk]
% Evaluating and diplaying divergence of f
g = divergence(f,[x,y,z]);
disp('Divergence of f is = ')
disp(g)
% Ploting 3-D graph
[X,Y,Z] = meshgrid(-1:.3:1,-1:.3:1,-1:.3:1);
G1 = subs(f(1),[x,y,z],{X,Y,Z});
G2 = subs(f(2),[x,y,z],{X,Y,Z});
G3 = subs(f(3),[x,y,z],{X,Y,Z});
quiver3(X,Y,Z,G1,G2,G3)
xlabel('x-axis')
ylabel('y-axis')
zlabel('z-axis')Input
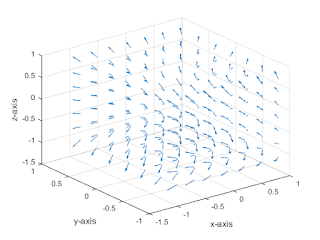
Enter a vector field: [x 2*y^2 3*z^3]
Output
Divergence of the function is =
9*z^2 + 4*y + 1
 |
| Divergence of x + 2y2 – 3z3 vector field in 3D figure |
Find divergence of two vector fields (x+y+z) and (u+v+w) in 3D figure MatLab
solution's code
load wind
g = divergence(x,y,z,u,v,w);
h = slice(x,y,z,g,[100 120],50,0);
shading flat
colorbar
daspect([1 1 1]);
axis vis3d
camlight
set([h(1),h(2)],'ambientstrength',0.6);Output
 |
| Divergence of two vector fields (x+y+z) and (u+v+w) in the 3D figure |
Divergence in 3D MatLab of a vector field
solution's code
syms x y;
prompt='Enter a i component of vector field: ';
x_in=input(prompt);
prompt='Enter a j component of vector field: ';
y_in=input(prompt);
% plot figure 1 vector field
figure(1)
[X, Y] = meshgrid(-2:.4:2, -2:.4:2);
F1=subs(x_in, [x y], {X, Y});
F2=subs(y_in, [x y], {X, Y});
set(gcf, 'units', 'normalized', 'position', [0.6 0.2 0.35 0.4]);
quiver(X, Y, F1, F2, 1, 'color', [0 0 1], 'linewidth', 2);
shading flat
xlabel('ix')
ylabel('jy')
title('x and y');
% claculate divergence
field = [x_in y_in];
vars = [x y];
div=divergence(field, vars);
% plot figure 2 divergence of vector field
figure(2)
set(gcf, 'units', 'normalized', 'position', [0.2 0.2 0.3 0.5]);
shading interp;
axis equal;
box on
view(-26,52);
fsurf(div, [-2, 2, -2, 2])
xlabel('x')
ylabel('y')
zlabel('divergence');
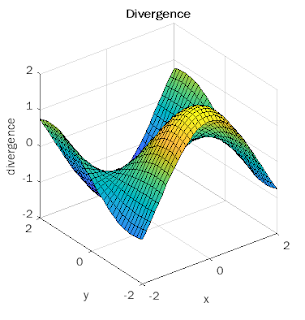
title('Divergence');
hold off
Input
Enter a i component of vector field: -sin(x)*sin(y)
Enter a j component of vector field: cos(x)*cos(y)
Output
 |
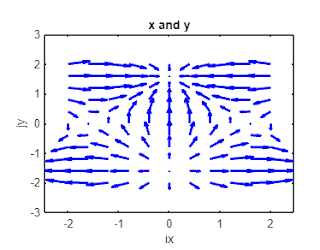| Figure 1: x and y values before divergence |
 |
| Figure 2: Divergence in 3D for a vector field |
Sources
1. https://www.youtube.com/watch?v=8VDoZXkOwGs
2. https://www.mathworks.com/help/matlab/ref/divergence.html
Learn more from youtube
1. 3D divergence in MatLab
2. Vector Field and Divergence Introduction
3. Divergence Theorem
Tags:
Matlab