The Breadth-First Search or BFS is a traversing or visiting type technique that can be used to color or visit graphs based on a real-life problem. The time complexity of BFS varies by implementation technique. Generally, the BFS time complexity is O (V + E). BFS time complexity using adjacency matrix is O (V * E). In this post, the time complexity of BFS will be discussed broadly.
Understand the BFS algorithm before the BFS Time Complexity
BFS Algorithm
 |
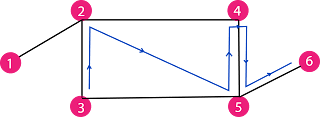
| Graph for BFS example (6 nodes) |
BFS code using Python
def bfs_algorithm(visited, graph, start_node):
# Mark the start node as visited
visited.append(start_node)
# Add start node to queue
queue.append(start_node)
# While the queue is not empty
while queue:
# printing all visited node list by popping queue
visited_node_list = queue.pop(0)
print (visited_node_list, end = " ")
# For all edges of the graph
for neighbour_node in graph[visited_node_list]:
# Check, If the neighbour node has not visited
if neighbour_node not in visited:
visited.append(neighbour_node)
queue.append(neighbour_node)
if __name__ == '__main__':
# Define the graph
graph = {
'1': ['2'],
'2': ['3', '4'],
'3': ['2', '5'],
'4': ['2', '5'],
'5': ['3', '4', '6'],
'6': ['5']
}
# initializing the visited variable
visited = []
# initializing the queue variable
queue = []
# Assigning the start node
start_node=input('Choose a start node from the graph (from 1 to 6): ')
print("Applying the Breadth-First Search Algorithm")
# Calling the Breadth-First Search
bfs_algorithm(visited, graph, start_node)Test 1:
 |
| Node visiting graphical view of the input graph (test 1) |
Test 2:
Time Complexity of BFS:
Considering the below graphs to find out the time complexity of the BFS algorithm. If there are V-th (V1, V2, V3, V4, V5, V6) vertex and E-th (E1, E2, E3, E4, E5, E6) edge.
V-th = V1+V2+V3+V4+V5+V6
E-th = E1+E2+E3+E4+E5+E6
Why should we use Big O notation?
As usual, we will use the Big O notation. So, the question is, why Big O notation? Because Big O notation is used to describe the run time or space requirements according to their / based on the problem input size. As the input size matter in the BFS technique and we want to find the run time complexity for this problem and that is why we will use the Big O notation. The Big O notation is mainly used as a way to calculate how long the algorithm will take to run without actually having to run it on the computer hardware. This notation is also compatible with clock speed, IPC(Instructions Per Cycle), and other factors in a computer.
We have to visit all the vertices and edges to complete the BFS technique of a graph. Then the time needed to visit all points one's need,
Time Complexity = O ((V1+V2+V3+V4+V5+V6)+(E1+E2+E3+E4+E5+E6))
= O (V-th + E-th)
= O (th will be considere as Total of V & E)
= O (V + E)
If we use the adjacency matrix for this problem then the edge and vertex will be used at a time.
BFS Time Complexity = O (V * E)
The vertex and edge will take the same time to traverse the graph at a time.
BFS Time Complexity = O (V * V)
= O (V2)
BFS algorithm implementation + BFS time complexity
Algorithm: (1. Add start node to queue)
Code: queue.append(start_node)
Time Complexity: O (1)
Algorithm: (2. While the queue is not empty (do the below steps))
Code: while queue:
Time Complexity: O (1)
Algorithm: pop(distance, current node) from the queue
Code: visited_node_list = queue.pop(0)
Time Complexity: O (1)
Algorithm: If the current node has not been visited (do the below statement)
Code: null
Time Complexity: null
Algorithm: Mark current node as visited with its distance
Code: visited.append(neighbour_node)
Time Complexity: O(1)
Algorithm: For all edges of the graph (current node, neighbour node)
Code: for neighbour_node in graph[visited_node_list]:
if neighbour_node not in visited:
Time Complexity: O (V+E)
Algorithm:If the neighbour node has not visited, add(distance+1, neighbour)
Code: queue.append(neighbour_node)
Time Complexity: O (1)
The space complexity of BFS (Breadth-First Search)
Depending on the graph representation, the space complexity of the breadth-first search may vary. If we know about the vertices value with properly calculated time complexity and also all vertices have been successfully appended to the queue, then the space complexity of the breadth-first search is O(V), where V is the total number of vertices in a graph.
The space and time complexity of BFS in a big graph
When working with a large number of vertices in a graph, the branches of the graph has been increased with the graph expansion. In that situation, we should have counted another factor which is called branching factor (b) with the distance between vertices (d). Now, the space complexity of the breadth-first search is O(bd+1). This effect also the time complexity of BFS. The time complexity in a big graph is O(bd+1).
Questions and Answering About BFS Time Complexity
Q1. What is BFS?
Ans: BFS is the short form of the Breadth-First Search algorithm.
Q2. What do you mean by the time complexity of BFS?
Ans: The BFS time complexity refers that the time needed to complete an operation in the BFS algorithm. To detect a cycle in a graph or find a specific node in a graph.
Q3. What kind of technique does the BFS algorithm follow?
Ans: The Breadth-First Search (BFS) algorithm follows the vertex traversing technique.
Q4. What is the time complexity of BFS?
Ans: The worst-case time complexity of BFS to traverse a graph is O(V + E).
Where alphabet V represents vertex and E represents edges of a graph.
Q5. What is the time complexity of BFS using the adjacency matrix method?
Ans: O (V * E)
Q6. If the time to visit a graph takes the same time for the vertex and edge of the graph. What will be the time complexity of the BFS algorithm?
Ans: O (V2)
Q7. What is the space complexity of BFS?
Ans: In terms of worst-case performance, the space complexity of BFS is O (V).
Q8. What do you mean by the space complexity of BFS?
Ans: The space complexity of BFS refers to the storage needed to run an operation using the BFS algorithm in a computer or system.
Q9. You want to calculate the time complexity of BFS in a Big-graph that has over 100 branches of each node. What will be the time and space complexity for that big graph if we use the BFS algorithm?
Ans: O(bd+1).
Here alphabet b represents the branching factor, and d represents the distance between vertices in a graph. We have already discussed it.
Q10. How can we optimize the BFS algorithm to reduce its time complexity?
Ans: We can use the dynamic programming solution to reduce BFS time complexity. Moreover, we can use another array to store the visited node and prevent the revisited node process.
Q11. Is there any way to reduce the space complexity of the BFS algorithm in the running time?
Ans: Yes. We can use the adjacency matrix to reduce the memory size in the running time of Breadth-First Search.
Q12. When should we apply the BFS algorithm?
Ans: The BFS algorithm is more practical to find a cycle in a graph or detect adjacent nodes.
Q13. What is the time complexity of removing or adding a vertex in BFS?
Ans: The time complexity of BFS to remove or add a vertex in a graph is O(1). The time complexity will change when you do that for a group of vertices. The time complexity to remove or add vertices using BFS is O(V). That is also the same in terms of the edges list. So, Removing or adding vertices or edges in BFS is O(V) + O (E).
Q14. What is the 'search key' in a traversing algorithm like BFS?
Ans: Sometimes, the Start-Node of a graph is called the 'search key' in a traversing algorithm.
Q15. What will occur if we apply the BFS algorithm in Artificial intelligence (AI) system?
Ans: The graph will be infinite in an AI system. We have to take the input of BFS as an implicit representation if we want to apply the traverse successfully.
Q16. What will happen if we apply the BFS algorithm in an infinite graph?
Ans: The BFS algorithm applied in AI technology. This algorithm can traverse an infinite graph successfully. Also, it will return to its search key position without any error.
Q17. What are the applications of a BFS algorithm in the computer science area?
Ans:
1. To compute the maximum flow in a graph using the Ford-Fulkerson method.
2. To find the shortest path in a network or graph.
3. To implement the parallel algorithms.
4. To copy garbage collection in the automatic memory management system.
Q18. What is the use of queue in the BFS algorithm?
Ans: Queue applies in the BFS algorithm to use some extra memory to track child nodes in a graph.
Q19. How does the Breadth-First Search (BFS) algorithm help the gamer in Chess-game?
Ans: At the end of a chess game, the BFS algorithm finds all possible moves to win the game from the current position on the chessboard.
Q20. What is 0-1 BFS (zero-one Breadth-First Search)?
Ans: This type of BFS uses to find the shortest path or distance between two nodes (source node to destination node) in a graph with edge values of 0 or 1.
Q21. Can we use a queue in all types of BFS algorithms?
Ans: Queue is necessary to store the child node in a graph. We can't use a general queue in the 0-1 BFS algorithm. The 0-1 BFS algorithm needs to remove top elements and insert the node at the beginning and end. A general queue can't do those operations.
Q22. Why can't we use a stack in BFS?
Ans: We need to store the node lists to traverse in a graph and retrieve them in a particular order using BFS or DFS algorithm. For a BFS, a stack does not return the items to search next in the correct order. A queue, on the other hand, does.
Q23. In which type of graph BFS is more applicable than DFS?
Ans: A BFS is more efficient than a DFS in finding the shortest path in an unweighted graph.
Q24. How does a BFS work on Facebook Website?
Ans: Each user profile treats as a node on the Facebook Website graph, and two nodes are said to be connected if they are friends with each other.
Q25. Can we use the BFS algorithm in all social networks?
Ans: Most social networks use the BFS algorithm in the backend part. As we mentioned before, the user considers like a node in a social network.
I would like to recommend a youtube video for a better understanding of Breadth-first Search (BFS).
Time distribution of this video: (00:40 Graph search, 02:00 Recall graph, 05:20 Applications of graph search, 10:30 Pocket cube 2x2x2 example, 20:25 Graph representations, 20:40 Adjacency lists, 26:00 Implicit representation of graph, 29:05 Space complexity for Adjacency list, 31:05 Breadth-first search, 34:05 BFS pseudo-code, 36:58 BFS example, 43:27 Shortest path, 48:35 Running time of BFS).
Read Similar Posts:
3. Insertion Sort Time Complexity