Prim's algorithm is a minimum spanning tree used to find the minimum path with minimum cost in a weighted graph. The implementation of this algorithm is complicated than Kruskal's algorithm. That is why its time complexity is also high than Kruskal's algorithm.
Prim's Algorithm Time Complexity
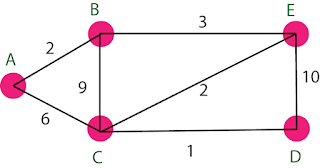
Considering the below-weighted graph to describe the time complexity of Prim's Algorithm properly.
Fig. 01: Graph for Prim's Algorithmhm
There are n-th vertices and m-th edges. The value of n and m is,
n = n-th vertices length
n = (A + B + C + D + E)
m = m-th veritces length
m = (AB + BC + .... + DE)
We have to traverse the graph using Prim's algorithm from the source point to the destination point until we find the minimum cost path or minimum spanning tree.
If we choose n-th vertices for n times and continuously elected grom graph to traverse. The complexity will be,
Time Complexity = O ( n-the visited vertices * m-th visited edges)
= O (A + B + ... + E) * (AB + BC + .... + DE)
= O (n * m)
= O (nm)
So, the time complexity of Prim's algorithm is O(nm).
Optimization technique
The time complexity O(nm) can be reduced to O(n2). Generally, we will start from the source vertex A and then we will check the 'A' related vertex that means B and C. We will check it each time we visited the A vertex. We can do the optimization here. When we will select the unselected vertex, we will select the minimum cost value vertex. This is how the optimization will be done and the time complexity of Prim's algorithm will be reduced from O(nm) to O(n2).
Read Similar Posts:
3. Insertion Sort Time Complexity
5. Linear Programming Time Reduction
6. Dijkstra Algorithm Time Complexity